Tackling Associative Arrays in Symbolic Execution
Recently as part of a small project I have been wondering what is the most efficient data structure for implementing associative arrays when symbolic keys are involved.
An associative array is a data type consisting in a collection of key-value pairs such that each key in unique. Normally this data type allows for operations such as lookup, insertion, removal and modification of values associated with a given key. This key-value storage paradigm is pretty common in computer science and often known with the name of dictionary or map.
Associative arrays can in principle be implemented using a large variety of data structures: search trees, hash tables, sorted lists, direct-indexed arrays, skip lists, etc. Most of the data structures employed for associative arrays offer overall logarithmic complexity for the most common operations with some of them, like direct-indexed arrays and hash tables, having constant or close to constant complexity.
Nothing very new so far. But now let’s combine associative arrays and symbolic execution and let the headaches begin.
How does symbolic execution work ?
If you are not familiar with the concept of symbolic execution I strongly suggest you to have a fast look at this wikipedia article. In any case I will try to give a simple example in order to understand what symbolic execution is about.
Let’s consider the following code:
1
2
3
4
5
6
7
8
9
if (user_input > 42){
if (user_input < 100){
// Path 1
} else {
// Path 2
}
} else {
// Path 3
}
Depending on value of the variable user_input this program can follow three different execution paths.
The way symbolic execution work is by associating to a given value a set of constraints during execution. For example if we consider user_input as a symbolic value then an hypothetical symbolic execution engine will be able to understand that this value needs to meet the constrains > 42 and < 100 in order for the first path to be executed.
In fact that’s what would normally happen during symbolic execution: when the first condition is encountered the execution is forked in two states, one having the user_input > 42 constraint and the other having the user_input <= 42 constraint. Each state continues its execution independently.
When the second condition is encountered the first state will be forked again in two separate states, each one adding an additional constraint. We will have at this point three different executions, which constraints are respectively user_input > 42 && user_input < 100, user_input >= 100 and user_input <= 42.
Given this ability of exploring different execution paths, symbolic execution is often used for testing purposes. However you can clearly see that the higher is the number of conditions encountered during execution the higher will be the number of potential paths and subsequent forks during symbolic execution. This introduces one of the most famous limitations of symbolic execution: the path explosion problem.
The name says it all, if the program under test has too many possible execution paths the number of states will explode and exploring every path symbolically will become unfeasible.
Boring intro to symbolic trees
Now let’s investigate a little bit on what would happen if we decide to use symbolic keys in an associative array. For simplicity let’s imagine that the associative array is implemented as a binary search tree and suppose that the symbolic key is initially unconstrained.
Lookup with symbolic key and concrete tree
Let’s consider this simple instance of well-balanced binary search tree, with seven nodes.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
18
/ \
/ \
/ \
/ \
/ \
/ \
/ \
13 30
/ \ / \
/ \ / \
/ \ / \
/ \ / \
10 15 22 35
Each node is associated with a key which will in turn be used to lookup the corresponding value. Here we don’t care much about the value associated to the key, but rather the key itself. Given for example a lookup key of 10, the lookup routine will start by comparing 10 with the root 18 and explore the left branch of the tree and so on and so forth until the leaf having 10 as key is reached.
In practice most libraries implement node search as follow:
1
2
3
4
5
6
7
8
9
10
11
while (node != NULL) {
int cmp = compare_key(node->key,mykey);
if (cmp == 0) {
return node; // successful lookup
} else if (cmp < 0) {
node = node->left;
} else {
node = node->right;
}
}
return NULL; // failed lookup
…so to keep things simple for now on we will stick to this kind of implementation.
But what happen if the lookup key is symbolic? Then every possible execution path will be explored. In particular since there are seven keys in the tree we can assume there are at least seven execution paths. However we should also consider all execution paths that result in a failed lookup, in total there are eight (one for each intermediate value).
For example: a symbolic key with constraint < 10 will reach the leftmost leaf and fail just after going left (node = node->left) while a symbolic value with constraint > 10 and < 13 will still reach the node having 10 as key but this time will fail just after going right (node = node->right).
This leaves us with a total of 15 possible execution paths for such small tree!
Insertion of symbolic key in concrete tree
If we decide to insert a symbolic key into the tree then once again we will have 15 possible execution paths. Seven execution paths for the case when our symbolic key hits a preexisting key plus eight new possible leaves in the tree:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
18
/ \
/ \
/ \
/ \
/ \
/ \
/ \
13 30
/ \ / \
/ \ / \
/ \ / \
10 15 22 35
/ \ / \ / \ / \
s1 s2 s3 s4 s5 s6 s7 s8 <-- eight possible new symbolic leaves
Lookup of symbolic key in symbolic tree
Going back to the lookup, what would happen if we want to lookup a value after inserting a symbolic node ? Let us consider the following tree, where the leaf s3 is a symbolic value having as constraint s3 < 15 && s3 > 13:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
18
/ \
/ \
/ \
/ \
/ \
/ \
/ \
13 30
/ \ / \
/ \ / \
/ \ / \
10 15 22 35
/
s3 (s3 < 15 && s3 > 13)
As before we have as many execution path as elements in the tree plus the number of intermediate values (which is usually equal to the number of nodes plus one). Therefore 17 execution paths.
However something interesting happens when the symbolic key for the lookup meets the symbolic leaf stored in the tree: the symbolic expression of the first will reference the constraints of the latter (or vice versa). This will cause the symbolic expression of the new value to grow in size.
Multiple lookups and/or insertions
You probably already guessed it: the number of execution paths after each symbolic operation grows exponentially. Taking the simple example of the key lookup, after a single key lookup our program forked in 15 different execution. If a second key lookup is performed then each of those 15 executions will fork again to 15 different executions and we will end up with 225 execution paths. After only three lookups we will have 3375 executions and so on and so forth…
Symbolic execution and associative arrays
We have seen how symbolic lookups and insertions behave using a binary search tree. Symbolic search operations are pretty expensive but can we make things somehow better ?
Yes and not. The exponential growth of the number of paths is inherent to the paths exploration problem itself and cannot be improved if not with some insights on the program we are running. However we could improve on the overall number of paths for a symbolic operation or maybe even on the quality of the symbolic expressions.
Removing useless paths
We have seen that for our simple tree with seven nodes a simple symbolic lookup would explore 15 paths, but how many of those paths are actually useful ? Seven paths out of 15 are used to reach the nodes in the tree, however the remaining eight paths are all “missed” searches, each one having different constraints.
Maybe we can merge them in a single paths representing all possible “missed” lookups…and turns out linked lists are exactly what we need.
The revenge of linked lists
Unsorted linked lists are one of the simplest data structures one could ever think of. Let us consider this linked list containing exactly the same elements of our little tree:
1
START --> 18 --> 15 --> 13 --> 30 --> 22 --> 10 --> 35 --> END
A lookup will start by comparing the symbolic lookup key to 18, then to 15, then to 13 etc. Every unsuccessful lookup will eventually end up in the same exit point END. Therefore this time we will have exactly eight execution paths instead of 15.
But will this translate is an actual improvement in terms of execution speed? Let’s try it out.
In order to benchmark symbolic execution with different data structures I decided to use KLEE together with a C library implementing well balanced binary trees. My choice has fallen upon libdict since it provides many variety of binary trees and other data structures. Unfortunately libdict does not provide a simple linked list, however we can easily implement one ourself and add it to the library (beside, we just need the search and insert operations).
In particular libdict wants us to give a comparison function taking as input two pointers to the two key to compare and returning a value of zero, if the keys are equal, or a negative or positive value if the first value is respectively smaller of bigger than the second.
Here is an example:
1
2
3
int cmpuint(unsigned int *a, unsigned int* b){
return (*a < *b) ? -1 : (*a > *b);
}
Without any doubt this function to compare two unsigned int would work in a normal context, but not in our case. This functions contains itself three execution paths.
When executing this function with a symbolic argument KLEE will eventually try to explore every possible path. Can we create a comparison function returning three possible outcomes, yet having only one execution path? Yes we can.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#define SHIFT_SIZE1 ((sizeof(long int)*8)-1)
#define SHIFT_SIZE2 ((sizeof(unsigned int)*8)-1)
int cmpuint(unsigned int *a, unsigned int* b){
// Compute difference
long int d = ((long int) *a - (long int) *b);
unsigned char* p = (unsigned char*) &d;
// Set sign bit
unsigned long int x = (unsigned long int) d;
int r = (int) (x >> SHIFT_SIZE1) << SHIFT_SIZE2;
// Set least significant bits using the difference
r |= p[0] | p[1] | p[2] | p[3] | p[4] | p[5] | p[6] | p[7];
return r;
}
It is not the most beautiful/understandable syntax for such simple task, but it does the job. Now, let’s compare the performances of an AVL-tree. with those of our linked list:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| AVL-TREE |
|--------------------------------------------------------------------------------|
| Nb elements in the array | Nb symbolic lookups | Paths executed | Time elapsed |
|--------------------------|---------------------|----------------|--------------|
| 10 | 1 | 21 | 0.57 s |
| 10 | 2 | 441 | 1.22 s |
| 10 | 3 | 9261 | 13.70 s |
| 10 | 4 | 194481 | > 3 m |
| 50 | 1 | 101 | 5.00 s |
| 50 | 2 | 10201 | 60.29 s |
| UNSORTED LINKED-LIST |
|--------------------------------------------------------------------------------|
| Nb elements in the array | Nb symbolic lookups | Paths executed | Time elapsed |
|--------------------------|---------------------|----------------|--------------|
| 10 | 1 | 11 | 0.36 s |
| 10 | 2 | 121 | 0.57 s |
| 10 | 3 | 1331 | 3.34 s |
| 10 | 4 | 14641 | 47.03 s |
| 50 | 1 | 51 | 1.43 s |
| 50 | 2 | 2601 | 16.70 s |
Great, we have an improvement. Who would ever have imagined that such primitive data structure would be better than AVL-trees when executing it symbolically.
However we didn’t forget our classes in computer science and clearly remember that there is a reason why we don’t use simple linked lists for big amounts of data entries: they are too slow. Is there a way to (more or less) keep the performance of linked lists while having the logarithmic complexity of AVL-trees ? Let’s try.
Scaling to bigger storages
In order to be able to execute symbolic queries on a binary tree with performance comparable to those of the linked list we can simply create a wrapper that differentiates between lookups resulting in a “hit” and those resulting in a “miss”. We can then manually craft a separate execution path that collect all the unsuccessful lookups.
Here is the code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// Create hit flag
int is_hit_se;
klee_make_symbolic(&is_hit_se,sizeof(int),"is_hit_se");
// Fork exec
if (is_hit_se) {
// Hits
void** datum = dict_search(dct, se);
if (datum == NULL) exit(0); // Stop execution with miss
} else {
// Assume symbolic value different than all keys in storage
dict_itor *itor = dict_itor_new(dct);
dict_itor_first(itor);
for (; dict_itor_valid(itor); dict_itor_next(itor)){
klee_assume(cmpuint(dict_itor_key(itor), se) != 0);
}
dict_itor_free(itor);
}
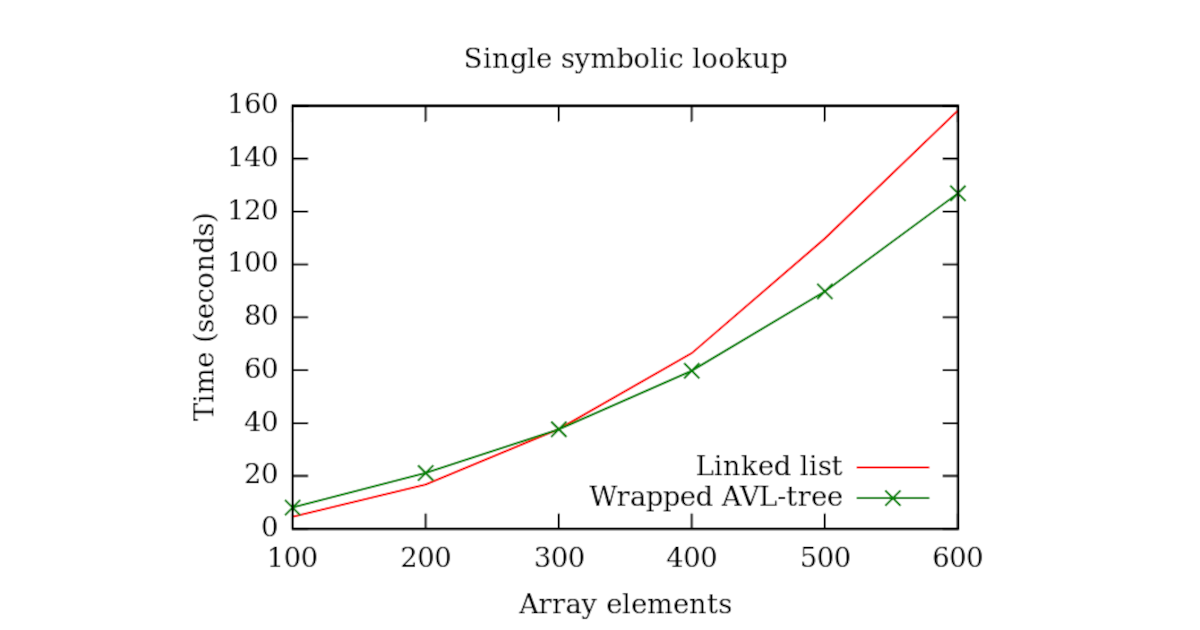
Let’s now see how a single symbolic lookup on an array with bigger size performs in both linked list and the AVL-tree with our wrapper.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| UNSORTED LINKED-LIST |
|--------------------------------------------------------------------------------|
| Nb elements in the array | Nb symbolic lookups | Paths executed | Time elapsed |
|--------------------------|---------------------|----------------|--------------|
| 100 | 1 | 101 | 4.55 s |
| 200 | 1 | 201 | 16.78 s |
| 300 | 1 | 301 | 37.77 s |
| 400 | 1 | 401 | 66.39 s |
| 500 | 1 | 501 | 109.84 s |
| 600 | 1 | 601 | 158.21 s |
| WRAPPED AVL-TREE |
|--------------------------------------------------------------------------------|
| Nb elements in the array | Nb symbolic lookups | Paths executed | Time elapsed |
|--------------------------|---------------------|----------------|--------------|
| 100 | 1 | 203 | 8.01 s |
| 200 | 1 | 403 | 21.14 s |
| 300 | 1 | 603 | 37.64 s |
| 400 | 1 | 803 | 59.74 s |
| 500 | 1 | 1003 | 89.78 s |
| 600 | 1 | 1203 | 126.90 s |
Let’s plot it:
We can see that for small amounts of concrete elements in the array the execution time of the wrapped AVL-tree is slightly worse than that of the linked list. However as the number of elements in the array increases the wrapped AVL-tree performs better if compared to the linked list.
We could go even further and, given the relatively small number of symbolic operation, use a separate linked-list storage for the symbolic values inside the database.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
// Create hit flag
int is_hit_se;
klee_make_symbolic(&is_hit_se,sizeof(int),"is_hit_se");
// Fork exec
if (is_hit_se) {
int hits_concrete_se;
klee_make_symbolic(&hits_concrete_se,sizeof(int),"hits_concrete_se");
// Hits
if (hits_concrete_se) {
void** datum = dict_search(dct, se);
if (datum == NULL) exit(0); // Stop execution with miss
} else {
void** datum = dict_search(sym_dct, se);
if (datum == NULL) exit(0); // Stop execution with miss
}
} else {
// Assume symbolic value different than all keys in storage
dict_itor *itor = dict_itor_new(dct);
dict_itor_first(itor);
for (; dict_itor_valid(itor); dict_itor_next(itor)){
klee_assume(cmpuint(dict_itor_key(itor), se) != 0);
}
dict_itor_free(itor);
// ... and also symbolic keys
list* ls = (list*) sym_dct->_object;
list_elem* el = ls->first;
for (; el != NULL; el = el->next){
klee_assume(cmpuint(el->key, se) != 0);
}
}